Understanding the Fibonacci Sequence: Nature’s Mathematical Marvel

The Fibonacci sequence is one of the most fascinating and widely recognized patterns in mathematics. Its simplicity and the multitude of natural phenomena it describes make it a captivating subject for both math enthusiasts and curious minds alike.

What Is the Fibonacci Sequence?

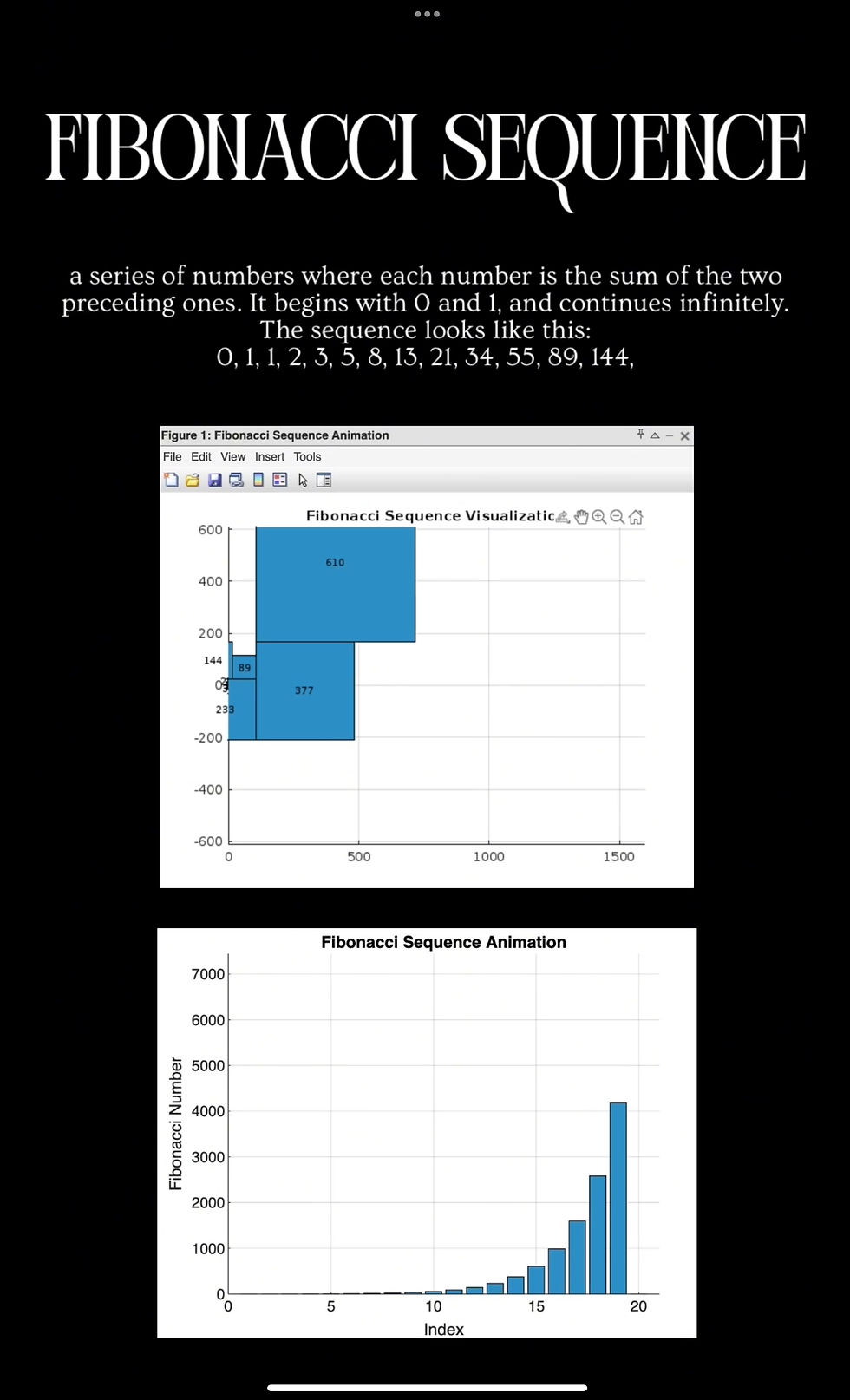
The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones. It begins with 0 and 1, and continues infinitely. The sequence looks like this:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

How Is It Formed?

The sequence is generated by the following recursive formula:

F(n) = F(n-1) + F(n-2)

where:

- F(0) = 0

- F(1) = 1

Each subsequent number is obtained by adding the two numbers before it. For example:

• 2 = 1 + 1

• 3 = 2 + 1

• 5 = 3 + 2

• 8 = 5 + 3

and so on.

spirals in nature

Why Is It Important?

The Fibonacci sequence isn't just a mathematical curiosity; it appears extensively in nature and art. Its significance lies in the patterns and proportions it creates, which often align with aesthetically pleasing and naturally efficient forms.

Fibonacci in Nature

- Plants: The arrangement of leaves, petals, and seeds often follow Fibonacci numbers. For example, sunflower seed heads display spirals in Fibonacci counts, optimizing packing efficiency.

- Shells and Spirals: The shells of nautilus and the horns of certain animals grow in logarithmic spirals related to Fibonacci ratios.

- Galaxies: Some spiral galaxies exhibit patterns that approximate Fibonacci spirals.

Fibonacci and the Golden Ratio

As the sequence progresses, the ratio of consecutive Fibonacci numbers (F(n+1)/F(n)) approaches the Golden Ratio, approximately 1.618. This ratio is famed for its aesthetic properties and appears in architecture, art, and nature.

spirals in nature

Applications and Significance

Beyond natural patterns, Fibonacci numbers are used in:

- Computer Algorithms: Sorting and searching algorithms.

- Financial Markets: Technical analysis and modeling.

- Art and Design: Creating compositions based on pleasing proportions.

The Fibonacci sequence is a beautiful example of how simple mathematical rules can generate complex and naturally occurring patterns. Whether in the arrangement of sunflower seeds, the spiral of a seashell, or the proportions of famous artworks, Fibonacci numbers remind us of the deep connection between mathematics and the natural world.

Check out our instagram reel!

If you're interested in exploring this sequence further or visualizing its patterns, there are many resources and tools available to deepen your understanding of this remarkable sequence!